Effets relativistes en chimie quantique

Les effets relativistes s’appliquent aussi en chimie, en particulier en présence d’atomes lourds. Leur prise en compte entraîne une complexité théorique qui dépend de l’approximation retenue.

  1. Domaine des effets relativistes en chimie
  2. Au-delà de l’équation de Schrödinger
  3. Exemple du dimère de xénon
Paul Adrien Maurice Dirac (1902–1984)

Domaine des effets relativistes en chimie

Plus le noyau d’un atome est lourd, plus la vitesse d’un électron autour de sa charge est grande, au point de donner lieu parfois à des effets relativistes. On peut par exemple montrer au moins approximativement que la vitesse d’un électron dans l’orbitale 1s d’un atome est égale au numéro atomique Z (en unités atomiques, dans lesquelles la vitesse de la lumière c vaut 137,036 u.a.). On en déduit alors le tableau suivant, qui témoigne de l’importance des effets relativistes pour les atomes les plus lourds :

Li (Z = 3)Cl (Z = 17)Xe (Z = 54)Au (Z = 79)
v/c2 %12 %39 %58 %

Parmi les éléments importants affectés par les effets relativistes figurent les lanthanides (sur la 6e période du tableau périodique), les actinides (sur la 7e période), le platine (Z = 78), ou encore le plomb (Z = 82).

Au-delà de l’équation de Schrödinger

Ces effets relativistes ne sont pas décrits par l’équation de Schrödinger, car elle n’est pas invariante par la transformation de Lorentz. Chronologiquement, on peut lister les apports théoriques qui menèrent à sa modification :

  • relativité restreinte développée par Einstein en 1905 (la même année que son travail sur le mouvement brownien) ;
  • mécanique quantique (pour une particule) rendue compatible avec la relativité restreinte par Dirac en 1926 ;
  • généralisation au cas de plusieurs électrons par Breit en 1929 ;
  • électrodynamique quantique par Feynman, Schwinger et Tomonaga en 1948.

Partant de la fameuse équation d’Einstein pour l’énergie cinétique

E=mc^2

et de la formule donnant la masse en fonction de la masse au repos

m=\frac{m_0}{\sqrt{1-v^2/c^2}}

l’équation de Schrödinger peut être modifiée en menant à l’équation de Klein-Gordon :

\left(i\hbar\frac{\partial}{\partial t}-q\phi\right)^2\Psi=c^2\left[\left(-i\hbar\nabla-\frac{q}{c}{\mathbf A}\right)^2+m_0^2c^2\right]\Psi

où A est le potentiel vecteur et ϕ le potentiel scalaire. Cette équation est invariante par la transformation de Lorentz, en accord avec la théorie de la relativité. En revanche, elle n’est valable que pour un boson. C’est Paul Dirac qui l’utilisa pour le cas du fermion. Sa reformulation de l’équation de Klein-Gordon fit apparaître deux équations couplées via la fonction d’onde, l’une pour l’électron, l’autre pour le positron. Dans le cas des états stationnaires de l’électron, cette équation peut s’écrire :

(E-q\phi-\beta m_0c^2-c\mathbf{ \alpha\cdot\pi})\Psi=0

où α et β sont des matrices qui vérifient des relations d’anti-commutation. La fonction d’onde devient alors un vecteur à quatre composantes, deux grandes regroupées dans un premier spineur, et deux petites regroupées dans un second spineur. Quand la vitesse est négligeable devant celle de la lumière, on peut montrer qu’on retrouve bien l’équation de Schrödinger non relativiste. De plus, il est possible de réduire la dimension du problème à deux composantes seulement au moyen de projections appropriées (par exemple selon la méthode proposée par Koelling et Harmon en 1977).

Charles Galton Darwin a donné une solution exacte de l’équation de Dirac pour les ions hydrogénoïdes (à un seul électron). Dans ce cas, les effets relativistes entraînent une contraction de l’orbitale 1s, c’est-à-dire une augmentation de l’exposant de leur fonction exponentielle :

\zeta=\frac{Z}{\sqrt{1-Z^2/c^2}}

Au lieu d’une valeur de 79 pour l’or, l’exposant vaut alors environ 97, c’est-à-dire que la décroissance de la fonction est nettement plus rapide.

L’étude des systèmes à plusieurs électrons se fait généralement en approximant leur hamiltonien total par une somme d’hamiltoniens de Dirac à une particule et de l’interaction de Coulomb.

Exemple du dimère de xénon

Le xénon est l’élément à partir duquel les effets relativistes commencent à se manifester plus nettement. Un calcul numérique (DFT avec la fonctionnelle PBE) de l’état fondamental de cet atome en l’absence ou en présence des effets relativistes (ici uniquement scalaires d’après Koelling et Harmon, donc en négligeant le couplage spin-orbite) permet d’observer les effets sur l’énergie et la densité électronique.

XeDFT non relativisteDFT relativiste scalaireDifférence
Energie (Ry)-14468,33924-14894,240193 %
ε5s (Ry)-1,32925-1,450918 %

Les effets relativistes, et notamment la contraction spatiale déjà mentionnée, sont plus marqués pour les orbitales de type s (et p). Dans le cas du xénon de configuration [Kr] 5s2 4d10 5p6, on peut observer une contraction de l’orbitale 5s (ici approximée par l’orbitale du système sans interaction de Kohn-Sham) :

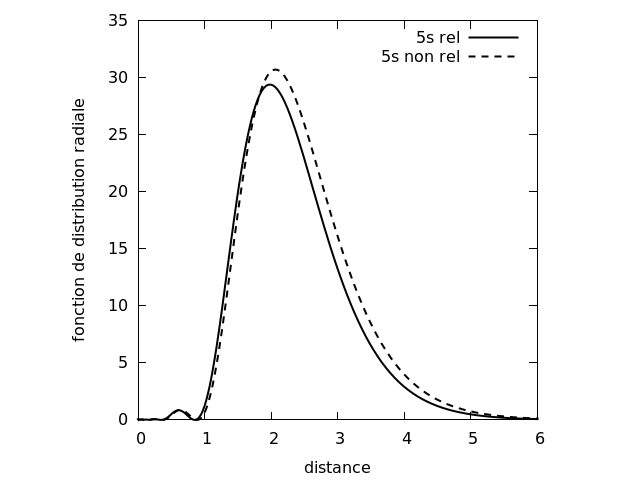
Dans le dimère, l’interaction de van der Waals est si faible qu’une grande précision dans le calcul est requise, aussi bien en terme d’effets de corrélation électronique que d’effets relativistes. Les premiers peuvent être inclus en utilisant par exemple la théorie de la fonctionnelle de la densité. Quant aux seconds, ils peuvent pour ce système se limiter aux effets scalaires. Quand on souhaite encore alléger le calcul pour envisager des simulations par dynamique moléculaire ab initio, il est aussi possible d’inclure ces effets relativistes scalaires par le biais d’un pseudopotentiel chargé de représenter les électrons de cœur, seuls les électrons de valence étant décrits explicitement, de manière non relativiste. On obtient alors un accord avec l’expérience raisonnable pour un coût de calcul modéré.

Xe2DFT-D3 relativiste scalaire (pseudopotentiel)Expérience
Energie d’interaction (kcal/mol)-0,566-0,561
Distance d’équilibre (Å)4,484,36
Au-delà de l’équation de Dirac

Pour rendre compte de la non immédiateté de l’interaction entre deux particules du fait de la finitude de la vitesse de la lumière, Breit introduisit une nouvelle équation qui a donné lieu à une approximation très utile : le hamiltonien de Breit-Pauli. Les termes qui le composent sont :

  • le hamiltonien non relativiste ;
  • un terme issu de la dépendance de la masse avec la vitesse ;
  • une interaction entre deux dipôles magnétiques orbitalaires ;
  • un couplage spin-orbite entre dipôles magnétiques ;
  • un terme non classique dit de Darwin ;
  • un couplage spin-spin électronique composé du terme de contact de Fermi et d’une interaction dipôlaire ;
  • l’interaction de Zeeman entre spins et champ magnétique externe.

Aller encore au-delà de cette équation fait appel à l’électrodynamique quantique.

Laisser un commentaire

L’auteur

Rodolphe Pollet est chercheur en sciences de la matière au CEA.

Rodolphe Pollet

Suggestions d’articles similaires